Matrices
especiales
El uso de las matrices es esencial en las matemáticas,
tanto que se utilizan en prácticamente todas sus disciplinas. Por esta razón,
existen propiedades y teoremas para matrices con una determinada forma. Por
ejemplo, el algoritmo de un ordenador que resuelve un sistema de ecuaciones
puede ser mucho más eficiente si la matriz es triangular, y todavía más, si la
matriz es diagonal.
Importante
-
Una matriz de dimensión nxn (mismo número de
filas que de columnas) es una matriz cuadrada de dimensión n
-
Si el número de filas y el de columnas son
distintos, la matriz es rectangular.
Tipos de matrices
Matriz identidad
Una matriz identidad o unidad de orden n es una matriz
cuadrada donde todos sus elementos son ceros (0) menos los elementos de la
diagonal principal que son unos (1). Además, la matriz identidad
se reconoce por tener forma a cuadrado dado que es una matriz cuadrada.
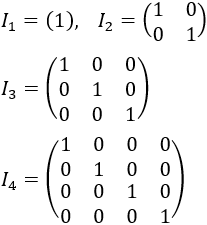
Matriz diagonal
una matriz diagonal es una matriz cuadrada en que las
entradas de las diagonales de la matriz son todas nulas salvo en la diagonal
principal, y éstas pueden ser nulas o no.
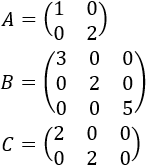
Matriz bidiagonal
Matriz tridiagonal

Matriz traspuesta
Una matriz traspuesta es el resultado de
reordenar la matriz original mediante el cambio de filas por columnas y las
columnas por filas en una nueva matriz.
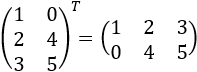
Matriz triangular
Es una matriz triangular superior si tiene 0's por debajo de la diagonal.
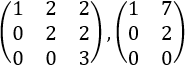
Es una matriz triangular inferior si tiene 0's por encima de la diagonal.
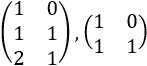
Matriz adjunta
Dada una matriz cuadrada A, su matriz de adjuntos o matriz
de cofactores cof(A) es la resultante de sustituir cada término aij de A por el
cofactor aij de A
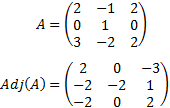
Matriz simétrica
Una matriz es simétrica si es igual a
su traspuesta, es decir, . Como
consecuencia
de la definición, la matriz tiene que ser cuadrada.
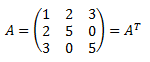
Matriz antisimétrica
Una matriz es antisimétrica si es la
matriz opuesta de su traspuesta, es decir, .
Como consecuencia de la definición, la matriz tiene que ser cuadrada.
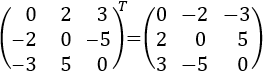
Matriz definida positiva
Una matriz A de dimensión mxn es definida positiva
si para todo vector x=(x1,...,xn)
se cumple
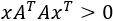
Si se cumple con la desigualdad ≥, diremos que la matriz es
semi definida positiva.
Una matriz cuadrada de dimensión es Hessenberg superior si todos los elementos bajo la diagonal -1 son nulos
Matriz diagonalmente dominante
Una matriz es estrictamente dominante
diagonalmente cuando los elementos de la diagonal principal son mayores en
valor absoluto, que la suma de los valores absolutos de los demás elementos de
la fila correspondiente.
Matriz Hessenberg
Una matriz cuadrada de dimensión es Hessenberg superior si todos los elementos bajo la diagonal -1 son nulos
Una matriz cuadrada A de dimensión n>1 es Hessenberg
inferior si todos los elementos sobre la diagonal 1 son nulos.
Matriz de Vandermonde
Es una matriz que presenta una progresión
geométrica en cada fila. Esta matriz recibe dicho nombre en honor al matemático
francés Alexandre-Théophile Vandermonde.
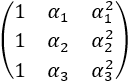
Ejemplo de una matriz Vandermonde de dimensión 4:
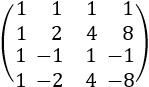



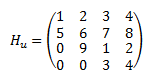
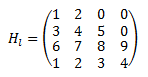
Comentarios
Publicar un comentario